In previous posts, I introduced the topics of task based parallelisation and Monte Carlo radiation transfer (MCRT). The topic of this week’s post will be my attempts at combining both. This algorithm forms the backbone of version 2.0 of CMacIonize and will hopefully be the subject of a code paper later this year.

MCRT tasks

To create a task based algorithm, we require tasks: small units of work that are only a small fraction of the total computational work and that use only a small amount of the computational resources: a single computational core and as little memory as possible. Since the MCRT algorithm requires a grid, it makes sense to base the MCRT tasks on a subdivision of this grid.

The grid is however only one component of the MCRT algorithm: we also have to think about the photon packets that are propagated through this grid. Photon packets are generated at a source, then travel through the grid for an unknown distance and in a random direction, before potentially scattering in a different random direction, leaving the box that encompasses the grid, or being absorbed. How do we fit these photon packets into the task based framework?

The solution is to again think about the grid. Photon packets only interact with the grid during one step of the MCRT algorithm: when they are being propagated for an unknown distance in a random direction. Generating the photon packets at the source does not require any knowledge about the grid. Scattering the photon packets (this can be because of direct scattering but also because of re-emission at a different wave length) requires some knowledge about the grid, but does not generally require access to the grid, i.e. it does not cause potential thread conflicts when done in parallel. So the only step of the MCRT algorithm that really requires unique access to a (part) of the grid is the propagation step.

When photon packets are propagated through a small part of the grid, they will likely leave the box encompassing that part before being absorbed, i.e. we cannot reasonably expect the photon propagation to be over once it leaves a single grid part. This is however not an issue, as all the information required to continue propagating a photon packet can be stored in a few variables: the current position of the photon packet, the current direction it is moving in, its current energy and the current optical depth it has accumulated while travelling through the grid. If we store these quantities in memory and read them back later, we can continue the photon propagation step in another part of the grid as if it never stopped. We can hence do the propagation step for a single part of the grid and on exit store the photon packet and continue its path later.

Storing single photon packets is however not very efficient, as there are typically many millions of them during a single step, and many of them access the same parts of the grid. It therefore makes sense to process photon packets in batches and store all packets in a batch within dedicated buffers. These buffers can be made to fit the memory requirements for a typical task by making them small enough, and can be handled in the same way as grid parts to make access to them thread safe.

With the introduction of photon packet buffers, the tasks that make up the task based MCRT algorithm can be defined as follows:

• photon packet generation: an empty photon packet buffer is filled with new randomly generated photon packets at a source
• photon packet traversal: the photon packets in a photon packet buffer are propagated through a part of the grid. On entry, all these photon packets are either within that part of the grid or entering it through one of its sides. On exit, the photon packets are either absorbed (and potentially scattered/re-emitted) within that part of the grid or leave the grid part through one of its sides, edges or corners (there are 4 sides and 4 corners for a 2D square cell and 6 sides, 12 edges and 8 corners for a 3D cubic cell). There are hence multiple possible output buffers for a single input buffer.
• photon packet scattering: a photon packet that was absorbed is scattered or re-emitted in a different direction and with potentially different properties.

The photon propagation step is illustrated below:

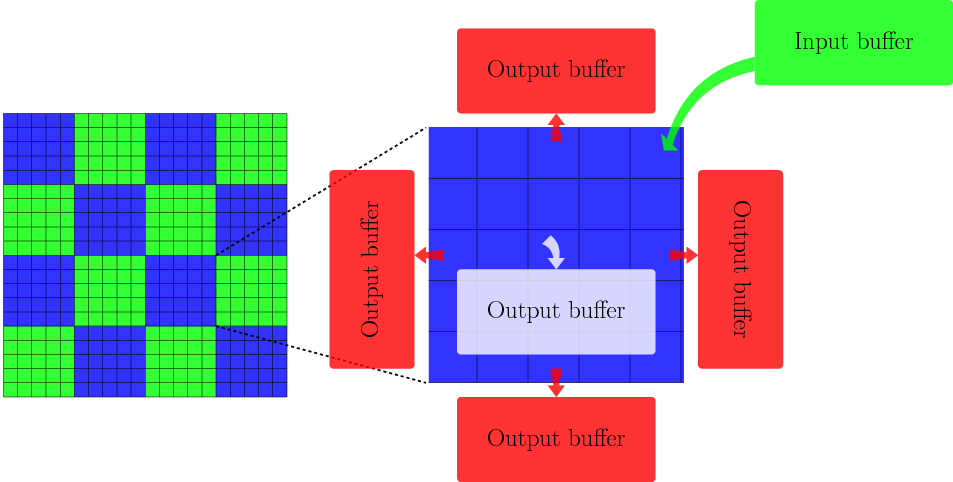
Below I will discuss the necessary components to turn these tasks into a working task based MCRT algorithm.

The distributed grid

The first important component in the task based MCRT algorithm is the grid that is split up into many smaller parts. I will refer to these parts as subgrids. Each subgrid has a number of neighbouring subgrids with which it shares a face, edge or corner, and to be able to efficiently process photon packets, this neighbour information needs to be stored. Each subgrid also requires a lock, i.e. some way of preventing multiple threads to access the subgrid at once.

Subgrids should as much as possible be self-contained, i.e. they should store all the geometrical information required to compute positions and volumes within the subgrid. They can however store this information in a compressed way, e.g. for a regular grid there is no need to store the volumes and coordinates of all cells; you only need to know the dimensions of the subgrid box and the number of cells within the subgrid.

Due to the strong non-local character of Monte Carlo radiation transfer, some parts of the grid (i.e. subgrids) are much more likely to be visited by photon packets than others, especially if the number of sources is low. This means that the locking mechanism that protects individual subgrids can potentially cause serious performance bottlenecks. To address this issue, it is possible to make subgrid copies: a subgrid that is visited a lot more than average is duplicated and the neighbouring relations for the neighbouring subgrids are adjusted so that half of the neighbours links to the original subgrid, and the other half to the copy. From the point of view of the individual subgrids, the algorithm can still proceed in the same way. At the end of the photon propagation step for all photon packets we can simply synchronise the optical properties between the copy and the original. This procedure can be repeated to generate more copies; I opted to do this using a power of two copy hierarchy, as shown below. In this hierarchy, each subgrid gets assigned a copy level $C$, and the number of copies for that subgrid is then given by $2^C$. Since all subgrids are small in memory, the duplication and synchronisation steps are very cheap and cause only a small overhead.

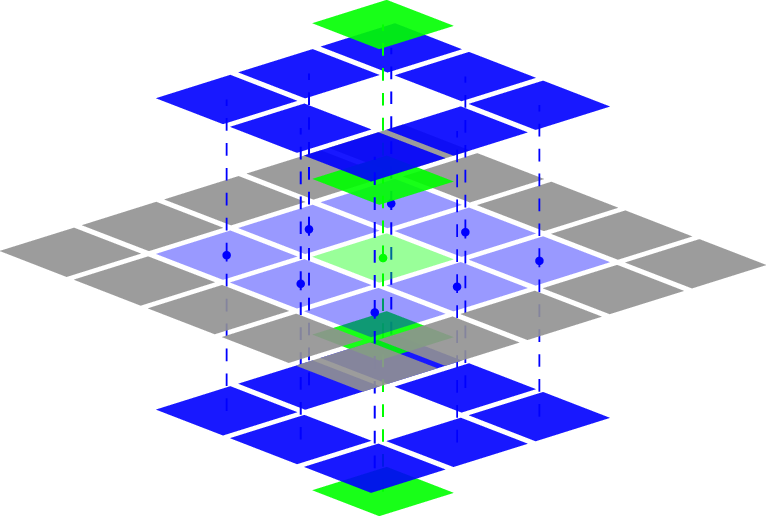
To determine optimal values for the number of subgrid copies, there are a number of options. One option is to keep track of the number of visits to each subgrid during a previous step of the MCRT algorithm and to use that value to refine the copy hierarchy dynamically. Although this is arguably the most correct method, it is quite tricky to implement and has a significant overhead. Furthermore, the load per subgrid tends to change between steps, so that this measurement is not necessarily representative enough. I therefore opted for more simple methods.

The least simple method consists of running a very low resolution MCRT simulation with little photon packets before the start of the actual simulation. Each subgrid in the actual simulation makes up a single cell in this low resolution simulation, and the optical properties of this cell are used to determine a good load for the corresponding subgrid. Despite its simplicity, this method performs surprisingly well, and is also the best method I have so far to perform the distributed memory load balancing for the task based MCRT algorithm. However, some overhead associated with the additional bootstrap simulation is clearly present, not in the least in the amount of additional code that needs to be written and checked. And I didn’t test this method in enough different scenarios to ensure that it always leads to a good load balance.

This is why I opted for an even simpler method for CMacIonize 2.0: a copy hierarchy based on the source positions. The main idea behind this is that subgrids with a high load are almost exclusively subgrids that either contain a source, or have a neighbour that does. We can flag the subgrids that contain a source and assign an arbitrary copy level to these (I currently use $C=4$, which correspond to $2^4=16$ copies). Next, we can ensure that subgrids that have a neighbour with a high copy level get assigned a high copy level as well, by e.g. limiting the copy level difference between neighbouring subgrids to 1. All of this can be done once, at the start of the simulation, and imposes very little overhead. Nevertheless, I found that it works very well.

A last subtlety about the use of subgrid copies is the treatment of source photons. Subgrids with a high copy level are almost exclusively subgrids that contain a source, and these subgrids get most of the photon packet load directly from photon packets originating at that source. To make sure the copies get a fair share of this load, we need to keep track of the number of copies of each subgrid that contains a source and distribute the photon packets from that source evenly among these copies. This requires some bookkeeping, but can be done without too much overhead.

Thread safe memory spaces

The task based MCRT algorithm introduced here has one big disadvantage compared to traditional task based algorithms like the one in SWIFT: the generation of additional tasks. Since we have no idea what subgrids will be visited by any given photon packet, we cannot a priori predict how many propagation tasks are required for each subgrid or what the task dependencies for these will be. The only way to get around this is by creating the propagation tasks when necessary, i.e. a task that is already running can spawn new tasks.

In itself this is not a problem for the execution of the tasks, as the task based locking mechanisms prevent unspawned tasks from being executed. It does however require us to implement an additional stop condition for the photon propagation step, as an empty queue for all threads does not necessarily mean the step is done. And it creates a significant issue with memory management for the resources that are used by the tasks: the tasks themselves and the photon packet buffers.

The tasks themselves are very small, but still require some variables to be stored: the type of task, the index of the subgrid they operate on, the index of the photon buffers involved (if any) and some locking mechanism to make sure only one thread can execute them. These variables require memory that needs to be allocated and managed. The same is true for the photon buffers; these are considerably larger in memory. I very quickly discovered that allocating the task and photon buffer memory when the task or photon buffer is created and deallocating it when it is no longer used is very slow. Furthermore, it causes huge bottlenecks, as memory allocations are almost always thread safe and hence very slow in a shared memory context. To avoid this, it is possible to preallocate a fixed amount of task and photon buffer memory at the start and reuse this during the simulation.

Managing preallocated memory requires some bookkeeping. First of all, it means that instead of handling tasks and photon buffers, we will be handling indices to these objects within the preallocated memory, and we need to pass on the relevant memory whenever we want to access task or photon buffer properties. Secondly, it means that we need to keep track of which indices are already in use and which ones are free. To make everything thread safe, we have to do these checks using a thread safe mechanism, i.e. we can use a lock for every element in the preallocated memory.

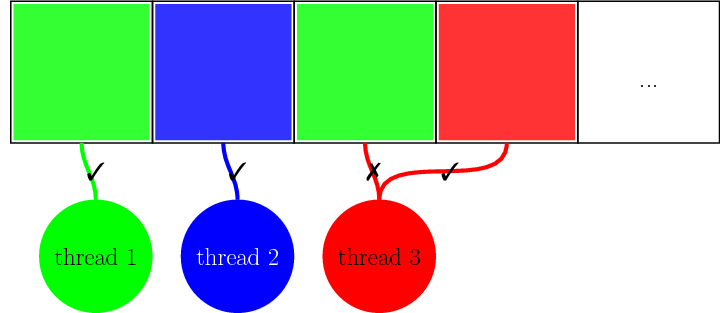
All of these requirements can be met by constructing a thread safe memory array as follows. First, a large block of memory is allocated with a fixed size that is chosen in advance (the current implementation does not allow changing the size at run time). Then, a shared memory lock is created for each element in the newly allocated memory block. Finally, an atomic index variable is created and set to point to the first element in the memory block. Atomic means that this variable can only be changed atomically, using low level CPU instructions that are guaranteed to be thread safe. So only one thread is allowed to change the value of the atomic index at any given time.

Then, we define three functions to deal with the elements of the memory block:

1. A function that returns a free element by repeatedly (a) atomically getting the old value of the index variable and incrementing it by 1, this guarantees that the current thread gets a unique index, and (b) trying to lock the corresponding shared memory lock, until locking the element succeeds.
2. A function that frees a previously obtained element by unlocking the corresponding shared memory lock.
3. A function that returns the element at a given index.

To make sure that freed up elements are reused, we wrap the index value modulo the memory block size. The entire procedure is illustrated in the figure below:

Partially filled buffers

A last important aspect of the task based MCRT algorithm is dealing with partially filled photon packet buffers. The size of a photon packet buffer is clearly quite arbitrary (I found that a value of 200 works well, but I do not have a good explanation for this particular value) and there is absolutely no guarantee that a buffer will ever end up being completely full, especially for subgrids that are far away from sources and near the end of the photon packet propagation step. If photon buffers were only propagated when they are full, then a lot of photon packets would end up not being propagated, which would invalidate the Monte Carlo technique. Or the algorithm would deadlock because it would never be able to process the partially filled buffers.

The solution is to prematurely schedule partially filled photon buffers in a smart way. In the current implementation, each thread first tries to obtain free tasks from its own task queue and execute those. If this fails, the thread will try to steal a task from another queue. If this fails too, it will try to get a task from a shared queue, which contains all photon source and scattering tasks. Only if this fails and the thread would otherwise end up being idle will it attempt to prematurely launch a partially filled photon buffer as follows. Each subgrid internally keeps track of the associated photon buffer with the largest number of photon packets. The idle thread starts with a reasonably high target number of photon packets, and will query all subgrids for their largest photon buffer size. Whenever it finds a subgrid whose largest photon buffer exceeds the target number, it will try to lock the subgrid and schedule the corresponding task for that photon buffer. If it fails to find a matching subgrid, it will reduce the target number and repeat the procedure, until a photon buffer has been scheduled.

Note that this premature scheduling routine is very sensitive to deadlocks and thread conflicts, as it is mainly active near the end of the photon propagation step, when most threads are idle and are desperately looking for work, like a hungry pack of hyenas looking for food. This means that proper locks should be used whenever required, but also that locks should be released as soon as possible, so that threads suffer as little as possible from concurrency bottlenecks. In other words, it is safe to assume that any work that shows up at this stage will be executed almost immediately, and likely by another thread than the one that schedules it.

Final remarks

The above gives a pretty good overview of the basic building blocks of the new task based MCRT algorithm I have developed. A few details were missing:

• I mentioned before that a dedicated stopping condition is required to determine when the photon propagation step is finished, as we cannot simply rely on all queues being empty. The appropriate condition in this case is that all photon packets that were generated were either definitively absorbed or have left the simulation box. This can be checked by updating an atomic counter variable for processed photon packets. Whenever a thread thinks it is finished (it is idle and is unable to prematurely schedule photon buffers), it checks this variable against the target number of photon packets; when both values match, the thread is finished. To make this compatible with a distributed memory version of the algorithm, where the atomic counter needs to be synchronised, I additionally check that total number of partially filled photon buffers is zero, as this can tell whether or not the local node is finished. Only when the node is finished do we perform a more expensive synchronisation of the atomic counter across all nodes.
• The memory spaces for the tasks and photon buffers need to be set at the start of the simulation. Clearly, a sufficiently large size is required for the algorithm to work. At the same time, we do not want to use a size that is much larger than what is strictly necessary to save memory. Although I have not yet done a proper analysis of the numbers, I discovered that the number of active photon buffers correlates with the number of threads used and the grid size. This number is a lot lower than the worst expected scenario (27 active buffers per subgrid). This means that relatively few photon packets are actively being propagated simultaneously. Note that this is depends strongly on the order in which tasks are retrieved from the various queues. Queue sizes can be variable, although I obtained good results with fixed queue sizes and relatively small queues for the individual thread (100 tasks per thread queue).

There are of course much more subtleties that I either forgot about, or that are just too technical for this post. It is not unlikely that I will discuss some of these in the future.