Python’s Matplotlib is a very powerful tool to make publication quality scientific plots, but its main strength is 2D (and 1D - I guess, but never really tried that) plots. Matplotlib does offer some 3D plotting functionality, but I have always found that this is not nearly as good as their 2D plotting capabilities.

In a way, this makes sense. If you think about it, 2D plotting is relatively easy: you have a 2D canvas and 2D data, so you simply need to put the 2D data on that canvas in some way and you have your plot. All the data will always be visible (unless it sits perfectly on top of each other, in which case you probably don’t need to see it anyway), and there is no need to trick the viewer into thinking they are looking at a 2D image, because, well, they are!

In 3D, the viewer will still be looking at a 2D image, but now this 2D image needs to contain information about a 3D data space. Depending on the viewing angle, data can now sit on top of other data without being at the same location in the actual 3D data space. Ensuring that the relevant parts of the data space are actually visible requires a careful selection of a viewing angle (or multiple viewing angles), while ensuring that the viewer actually perceives the data as being 3D requires a proper projection of the 3D data onto the 2D viewer canvas, combined with additional tricks that create a depth perception. Not only is this a lot harder to do than what is required to make a 2D plot (hence why Matplotlib, a library entirely written in Python, becomes too slow to do it efficiently), it also requires a lot more input from the person that creates the plot.

That is why, for 3D visualisation, I use other tools, like VisIt, that are faster and better suited to visualise and manipulate 3D data sets. These tools can be used via Python scripts, which makes them fit in well with my usual Python based workflows. They work fine for personal use, but the graphics they generate are usually not as nice to look at: they are okay for interpreting data, but I would not necessarily put these graphics in a scientific publication. The reason is that while they are excellent at projection 3D data into a 2D view, they are not very good at creating depth perception; the 3D nature of the data is obvious when you rotate a VisIt view in the program GUI, but is less clear if you only have a still image of that view to look at.

Fortunately, there exists a host of other open source software tools that are much better at generating truly 3D images. These tools add an additional step to the visualisation workflow: a rendering phase. During this phase, an actual simulation is performed of how light would interact with the 3D visualisation model of the 3D data until it is finally perceived by an observer that is located somewhere in the 3D space. Or in other words: the tool simulates what would happen if the 3D data was actually located in the 3D room where you (the viewer) are standing, and then figures out what you would see. This is an interesting metaphor to keep in mind for what I will explain later in this post.

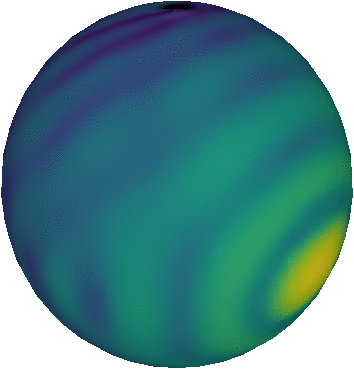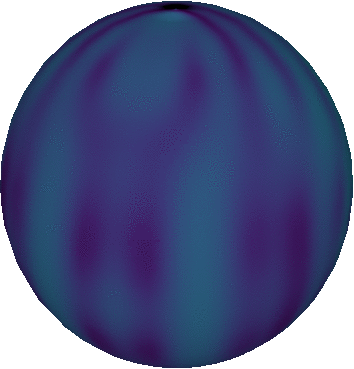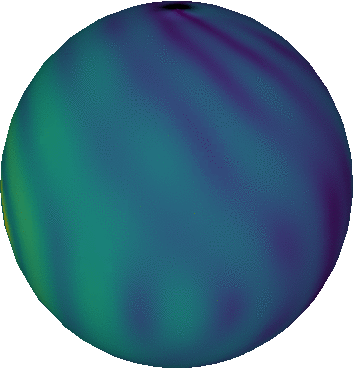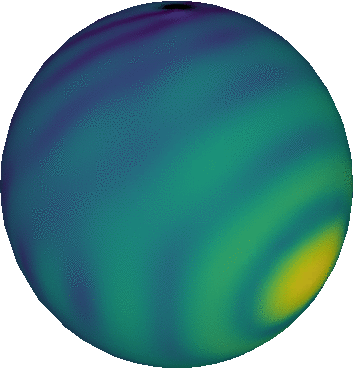
One of these tools is the open source 3D creation suite (as they call themselves) Blender. Blender is incredibly powerful: entire movies were generated using this tool. Just like VisIt, Blender has a Python API that makes it possible to use the program from a Python script. In this post, I will showcase the script I wrote earlier this week to make a plot of some angular data, i.e. I had a program that outputted some values as a function of two direction angles $\phi{}$ and $\theta{}$, and I wanted to know what that data would look like on a celestial sphere. The result is shown at the top of this page.

The non-scripted way

Before I start showing my script (which is about 200 lines long), I need to walk you through the steps that are required to actually generate this image. To generate the sphere itself, I used a so called UV sphere in Blender. This is not actually a sphere, but is a polyhedron that consists of a number of rings at equally spaced $\phi{}$ angles (along the equator of the sphere). Each of these rings is subdivided in a number of vertices for some values of the vertical angle $\theta{}$. It are those vertices, together with the straight edges that join them and the flat faces in between these edges that make up the sphere. The sphere only appears round because I use a sufficiently large number of vertices.

I told you before that Blender simulates what would happen if we put this sphere in an actual room. The only way we can actually put the sphere in a room, is by constructing it from something, i.e. we need a material to create the sphere. This might sound like killing the metaphor, but in Blender, this is also true: we can only simulate what would happen if the sphere was in a room, if we know what material the sphere is made of, since that material will dictate how light interacts with the sphere.

I don’t want to dwell too long on materials, so for our purposes it suffices to know that I will assume the sphere is made of a perfectly diffuse material, which means that light that scatters off the sphere will isotropically scatter in all directions. The colour of the material depends on the location on the sphere, and I obviously want this to depend on the data set I want to visualise. A map that specifies the colour for a material based on a location on an object is called a texture, so I need to provide an appropriate texture for the sphere.

If we think back about the room with the sphere, there is another thing that is missing before we can actually simulate how light interacts with the sphere: a source of light! Again, this might sound silly, but again, this is also true in Blender: if we want to simulate how light scatters off the sphere, we need to provide a light source. The location of that source within the 3D room will determine how the sphere is perceived, since parts of the sphere that are not directly exposed to the source will have shadows cast upon them.

As with materials, light sources come in many shapes and forms. I will use a light source at a single location of the type sun, i.e. a powerful light source that emits white light that is equally bright at all wavelengths.

The final thing missing from our metaphorical room is something that can actually observe the light that scatters off the sphere, i.e. a viewer. In Blender, the viewer is called the camera and a camera has to have a certain position, viewing direction and a certain size for its field of view. The location of the camera and the location of the light source are linked: if the light source and camera are on opposite sides of the sphere, then the sphere will simply block out all the light from the source, and no light will reach the camera. Since I want the entire visible surface of the sphere to be uniformly illuminated, I make sure the camera and the light source are at the same side of the sphere.

That’s it! Light from the source will illuminate the surface of the sphere, scatter isotropically with a colour that depends on the texture that contains the 3D data values, and some of it will scatter towards the camera and record a 2D image of the sphere. If I then slowly rotate the sphere around its vertical axis, repeat the rendering for these different positions, and paste all these images together, I get the animation on the top of this page.

The script

The Python script that generates the animation (or rather: the frames of the animation, as I used ImageMagick to put the frames together into a .gif.) is a combination of bits and pieces that I gathered from various places. Most of it is based on the excellent set of examples I found on https://github.com/njanakiev/blender-scripting. The entire script can be found in rotating_sphere.py.

Imports

At the top of the script, a number of modules need to be imported:

import bpy
import os
import numpy as np
import scipy.interpolate as interpol
import matplotlib as mpl
import matplotlib.cm as cm
import sys
import argparse

This list gives a good overview of the dependencies; all these modules will be used at some point during the script. The bpy module is the Blender Python API that contains all the Blender specific functionality. The numpy, scipy and matplotlib dependencies are all required to generate the colour map texture, as I will explain later.

Setting the scene

I will skip the part of the script that parses command line arguments and immediately move on to the bit of code that set the scene. The first thing to do is to remove all the objects already present in the default Blender scene (these are the same ones you get when you run the Blender GUI: a cube, a camera and a light source):

bpy.ops.object.select_by_layer()
bpy.ops.object.delete(use_global=False)

Next, we create a new target at the origin. This target will be used as a focus point for the camera we will create, and for the light source.

target = bpy.data.objects.new("Target", None)
bpy.context.scene.objects.link(target)
target.location = (0.0, 0.0, 0.0)

Now, we create a camera that looks at the target:

camera = bpy.data.cameras.new("Camera")
camera.lens = 35
camera.clip_start = 0.1
camera.clip_end = 200.0
camera.type = "PERSP"

camera_obj = bpy.data.objects.new("CameraObj", camera)
camera_obj.location = (-10.0, -10.0, 10.0)
bpy.context.scene.objects.link(camera_obj)
bpy.context.scene.camera = camera_obj
constraint = camera_obj.constraints.new("TRACK_TO")
constraint.target = target
constraint.track_axis = "TRACK_NEGATIVE_Z"
constraint.up_axis = "UP_Y"

And we add the light source:

bpy.ops.object.add(type="LAMP", location=(-10.0, -10.0, 10.0))
lamp_obj = bpy.context.object
lamp_obj.data.type = "SUN"
lamp_obj.data.energy = 1
lamp_obj.data.color = (1, 1, 1)
constraint = lamp_obj.constraints.new("TRACK_TO")
constraint.target = target
constraint.track_axis = "TRACK_NEGATIVE_Z"
constraint.up_axis = "UP_Y"

Finally, we create the sphere. I opted not to use the default UV sphere that Blender provides, but instead used a more general parametrisation of the vertices of the sphere that can also be used to generate spheroids and toroidal objects. This works better in combination with the texture we will apply later. To create the sphere, we first need to compute its vertex locations and face connections:

verts = list()
faces = list()
duv = 1.0 / nvert
u = np.linspace(0.0, 1.0 - duv, nvert)
v = np.linspace(0.0, 1.0 - duv, nvert)
ug, vg = np.meshgrid(u, v)
tau = 2.0 * np.pi
cosv = np.cos(tau * vg)
sinv = np.sin(tau * vg)
cosu = np.cos(tau * ug)
sinu = np.sin(tau * ug)
points = (6.0 * sinv * cosu, 6.0 * sinv * sinu, 6.0 * cosv)
for col in range(nvert):
  for row in range(nvert):
    point = (
      points[0][row, col],
      points[1][row, col],
      points[2][row, col],
    )
    verts.append(point)

    rowNext = (row + 1) % nvert
    colNext = (col + 1) % nvert
    faces.append(
      (
        (col * nvert) + rowNext,
        (colNext * nvert) + rowNext,
        (colNext * nvert) + row,
        (col * nvert) + row,
      )

Then, we create the actual object from this mesh of vertices:

mesh = bpy.data.meshes.new("SurfaceMesh")
sphere = bpy.data.objects.new("Surface", mesh)
sphere.location = (0.0, 0.0, 0.0)
bpy.context.scene.objects.link(sphere)
mesh.from_pydata(verts, [], faces)
mesh.update(calc_edges=True)

Finally, we make sure the sphere is rendered smooth by adding a so called modifier that doubles the number of vertices before rendering:

modifier = sphere.modifiers.new("Subsurf", "SUBSURF")
modifier.levels = 2
modifier.render_levels = 2
mesh = sphere.data
for p in mesh.polygons:
  p.use_smooth = True

Rendering the scene

In principle, we could already render the scene above. To do this, we need to set some rendering properties:

scn = bpy.context.scene
scn.render.resolution_x = resolution
scn.render.resolution_y = resolution
scn.render.resolution_percentage = 100.0
scn.render.alpha_mode = "TRANSPARENT"
scn.frame_end = nstep

render_folder = os.path.join(os.getcwd(), output_folder)
if not os.path.exists(render_folder):
  os.mkdir(render_folder)
scn.render.filepath = os.path.join(render_folder, output_prefix)
bpy.ops.render.render(animation=True)

Most of these are self-explanatory. Note that we set a transparent background for the image (everything that is not the surface of the sphere), and that we render the scene as an animation with nstep frames. All these frames will look the same, as we did not actually animate anything yet.

To generate the frames, we need to run the script. This is done using the following command:

> blender -b -P rotating_sphere.py

In other words: we have to run Blender itself, in the background (-b), and make it execute the Python script provided as the argument to the -P option. Note that the full script I provide requires additional command line arguments. These can be passed on at the end of this command by adding --, like this:

> blender -b -P rotating_sphere.py -- --file ARG1 --output-folder ARG2

If all goes well, a new folder rendering will be created that contains 100 frames with a static, white sphere.

Adding the texture

To create the texture for our sphere, we first need to create the texture image. This can be done in various ways, but the most efficient and clean way is to directly compute the pixel values from our input data (a simple text file with 3 columns: the $\theta{}$ angles, the $\phi{}$ angles and the data we want to map). First, we open the data file and parse the columns:

data = np.loadtxt(filename)
theta = data[:, 0]
phi = data[:, 1]
Zsingle = data[:, 2]

Next, we need to make sure the texture image we generate properly accounts for the curvature along a spherical surface. In practice, this means that we need to convert the $\theta{}$ angles to $\sin(\theta{})$, since the latter scales linearly along the curved surface:

theta = np.sin(theta - 0.5 * np.pi)

The input values could or could not be sampled on a regular grid in $(\theta{}, \phi{})$ or even $(\sin(\theta{}), \phi{})$ space. We need to make sure the pixels are sampled regularly in a $(\sin(\theta{}), \phi{})$ space by regridding:

gx, gy = np.meshgrid(
  np.linspace(phi.min(), phi.max(), npix),
  np.linspace(theta.min(), theta.max(), npix),
)
grid = interpol.griddata(
  (phi, theta), np.log10(Zsingle), (gx, gy), method="cubic"
)

The grid array now contains a single value for each pixel of the texture. To convert this into an actual colour map, we need to normalise the values and map them to RGBA colour values. For this, we use Matplotlib:

norm = mpl.colors.Normalize(
  vmin=min(np.log10(Zsingle)), vmax=max(np.log10(Zsingle))
)
mapper = cm.ScalarMappable(norm=norm)
pixels = mapper.to_rgba(grid)

This gives us an array of RGBA pixel values.

To create a texture from this, we need to create an empty texture image in Blender, and then overwrite its pixel values with the values we just computed:

textimg = bpy.data.images.new("TextureImage", width=npix, height=npix)
textimg.pixels[:] = pixels.flatten()
textimg.update()

Note that the pixel array needs to be flattened into a 1D array for this. Once the texture image has been created, we can create the texture, and add it to the material of the sphere:

spheretex = bpy.data.textures.new("SphereTexture", type="IMAGE")
spheretex.image = textimg
mat = bpy.data.materials.new("BumpMapMaterial")
mat.specular_intensity = 0.0
slot = mat.texture_slots.add()
slot.texture = spheretex
slot.texture_coords = "ORCO"
slot.mapping = "SPHERE"
sphere.data.materials.append(mat)

By setting mat.specular_intensity to 0, we ensure the material is perfectly diffuse. The slot.texture_coords and slot.mapping properties ensure that the texture colours are computed in the spherical reference frame of the sphere, i.e. that a proper coordinate conversion from 3D Cartesian coordinates to spherical coordinates is performed before applying the texture, and that the texture will move if the sphere itself moves.

With these additions to the scene, the rendered frames will now contain a sphere that has the desired colours. The frames will still all be the same however, since we did not animate the scene yet.

Animating the scene

To animate the scene, we require one additional directive in the main part of the script:

bpy.app.handlers.frame_change_pre.append(frame_change_handler)

This directive installs an event handler that is called whenever the renderer moves on to the next frame to render. This even handler is a function called frame_change_handler that looks like this:

def frame_change_handler(scene):
  global sphere, nstep, framecount
  sphere.rotation_euler = (0.0, 0.0, 2.0 * np.pi / nstep * framecount)
  framecount += 1

The scene argument to this function is obligatory and contains information about the frame that is currently being processed. We don’t use this information here. Our frame change handler simply computes a new angle for the rotation state of the sphere, which is then passed on to the rotation_euler property of the sphere. This will effectively rotate the sphere and its texture over 360 degrees in nstep steps when the function is called repeatedly for nstep times.